
# 自下而上投资的局限:经济活动的测不准原理
原创 沧海一土狗 [ 沧海一土狗 ](javascript:void\(0\);)
__ _ _ _ _
**

文/沧海一土狗 ** ** **
**引子**
不久之前,跟一位业内的老前辈聊天,谈论起了投资方法论的问题,是应该“自上而下”投资,还是应该“自下而上”投资?
由于我们两个都是做固定收益出身的,所以,对自上而下的投资方法有着天然的亲近感。当时,我也只是单纯地在自己的方法论里打转,前辈的一句话,让我有茅塞顿开的感觉:
> 自下而上的投资方法, ** 只适合宏观环境比较平稳的时候 ** ,当宏观环境变化剧烈的时候,这个方法会很惨,就比如今年。
基于这样的逻辑,我们不难推断,随着中国资本市场的开放,更多的国际因素会影响到国内宏观环境,造成其波动加剧,自下而上投资方法受到的限制会越来越大。
在现实中,有很多人喜欢给自己立flag——我就碰到过好多自称“自上而下”的基金经理。这些flag只给他们带来“抱团”的虚假安全感,环境一旦骤变,他们面临的只是团灭。
资本市场自然选择的力量是无情的,被工具绑架,不注重工具或者方法 **使用条件** 的人最终是要被淘汰的。
**宏观和微观的区别**
跟前辈的探讨激发了我更多的思考,宏观和微观的真实区别是什么?恰好在这段时间里,我读了一些物理学的科普读物,其中的案例以 **不同的视角**
向我展现了,宏观和微观的界限。
_**气体磁化实验** _
如果在一个长方形的石英管里注入氧气,并且把它放进磁场,你就会发现气体被磁化了。由于氧分子是一些小的磁体,于是,他们就会像指南针似的始终与磁场保持平行的趋势,这样我们就看到气体磁化的现象。
直觉上人们会认为它们都与磁场的单一方向平行,其实不是这样。如果你增加磁场,氧气中的磁化作用也随之增强,更多的氧气分子就会趋于这个方向。磁化效应会随着磁场强度的增加而增加,它们之间是一种正比例的关系。
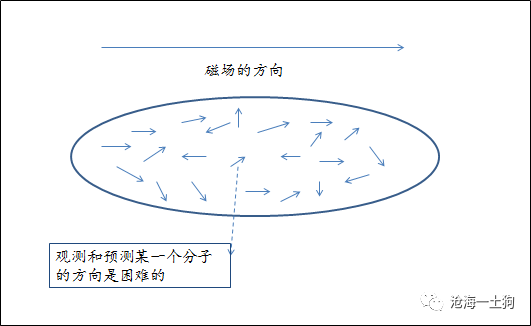
氧气分子的方向是杂乱无章的,他受两种力量的影响。宏观方面,单个氧气分子受到确定方向的磁场影响;微观方面,单个氧气分子不断地遭到 热运动
的随机取向的干扰。
尽管单个分子总是无休止的改变取向,然而,由于他们数量庞大,所以总体上来看,趋于场强方向的比例还是多于其他方向。
如何在物理上进一步验证统计假说呢?如果磁化现象的确是磁场力量和热运动随机干扰的某种平衡,那么,我们就 **可以通过降低温度来代替加强磁场**
。现实实验中,我们也的确发现了这一现象。
通过这个实验,我们可以发现,一方面,我们无法在微观上观测一些分子的朝向,也无法对他们的方向进行预测;另一方面,我们的确也能发现
**在宏观上存在一些确定的因果规律** 。微观的不可预测性和宏观的确定性以这样一种形式,完美地结合在一起。
除此之外,在布朗运动、扩散现象中,我们也可以发现,微观不确定性和宏观确定性的某种结合。在沉降的雾气中,微小的水珠运动轨迹表现出不规则的布朗运动,但是,受重力的影响,雾气总体还是分布在下层;在扩散运动中,虽然我们无法知晓某一个分子酒精分子的运动轨迹,但我们可以知晓酒精分子总体上会从浓度大的趋于扩散至浓度小的区域。
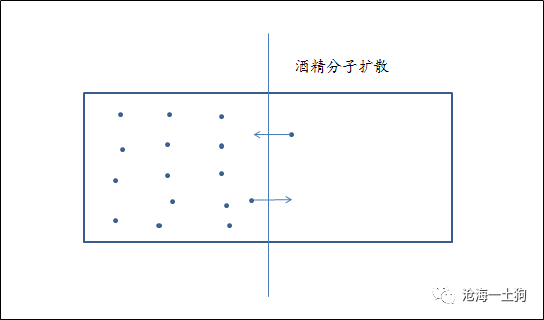
对于任意一个截面,任一个酒精分子从左侧穿越到右侧的概率,与从右侧穿越到左侧的概率是一样的。所以,当且仅当左侧酒精分子浓度和右侧酒精浓度一致时,宏观上来看,酒精浓度才不会出现变化;但是微观上来看,任意时刻总有一部分酒精分子从左侧运动到右侧,也有一部分从右侧到左侧,只不过
** 他们的数量接近一致罢了 ** 。
**尺度决定精度**
那么, **不可预测的微观个体是如何表现出确定性的宏观规律的呢?两者是如何的完美的结合在一起的呢?** 关于这一点,统计学可以给出一个解答。
对于n次掷硬币的实验(正面向上记成1,反面向上记成0),这个实验的期望EX=n/2,方差DX=n/4 。如果我们掷m次硬币,并
预测有多少次正面上,一个合理的预测就是他的期望m/2。
那么,这个 **预测的误差** 是多少呢?我们可以拿(标准差/期望)这个变量来计量误差,即误差是1/根号m
。也就是说,m越大这个预测越准,而且准度是以根号n的速度收敛的。( _ 所以,统计学上有个根号n原则 _ )
通过这个例子,我们就可以获得一种直觉,对于组成个体符合某种随机性的组合,组合越大,就越可能产生某种可以预测的行为,组合越小,就越受随机性的干扰。
> 尺度越大,预测越准。
>
> ——土狗按
**时效性和准确性的矛盾**
> 从长期看,我们都死了。
>
> ——凯恩斯
凯恩斯这句名言告诉我们,在某些问题上,单纯地追求准度——100%正确,对于我们可能毫无意义。现实中还有很多其他的例子,譬如,预测北京明年夏天一定会下雨,预测a股十年内一定会出现一波上涨。尽管这些预测会很准确,但他缺乏时效性。
现实当中, **人们除了会走准确度的极端之外,还会走时效性的极端**
。譬如,人们总是想预测明天的股市是上涨还是下跌?但是,因为尺度太小,预测的准度相当差,几乎相当于掷硬币。
在以前的文章《 [ 如何在充满噪音的世界里生存?
](http://mp.weixin.qq.com/s?__biz=MzUxNjE1NjI1MA==&mid=2247484472&idx=1&sn=e177f70eb522b146487f1e86c01dce9b&chksm=f9aafa0dcedd731b394d2303278b733e59d09c9611ef3f7036f01407bc62710d4e485a3ec3a3&scene=21#wechat_redirect)
》一文中,我们举过一个例子,我们这里再引用一下:
假设有一个投资高手,他一年期望的报酬率是15%,波动性(标准差)为10%,也就是说,一年下来这个投资高手的收益率大概率在5%和25%之间波动。
我们再假设他的报酬率符合正态分布的话,那么,他年收益落在5%和25%之间的概率为68%。此外,我们也可以很容易的算出,他年收益率大于零的概率为93%。
这时候就有一个很自然的问题,如果这个高手每季度看一次组合,他看到某一个季度组合收益上涨的概率是多少?
为了回答这个问题,我们再引入一个假设, **每季度的收益率独立同分布,** **且都是正态分布。**
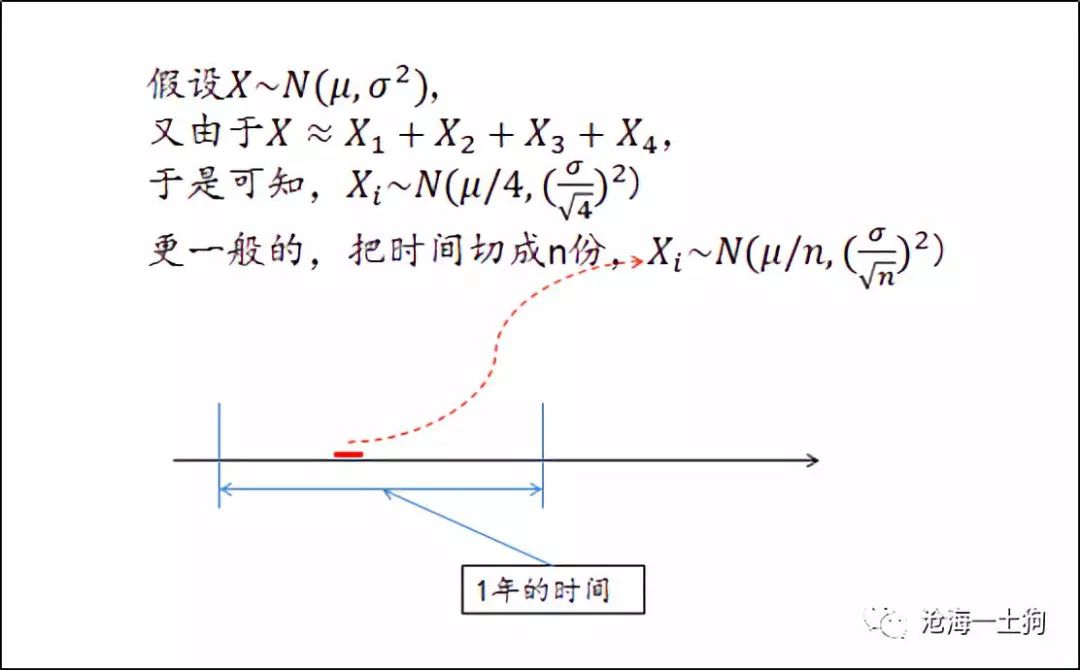
根据上面的数学推导,我们可以算出任意切片事件收益率的分布。然后,我们把参数代入公式,就可以计算在 ** 不同时间尺度上 ** ,赚钱的概率,
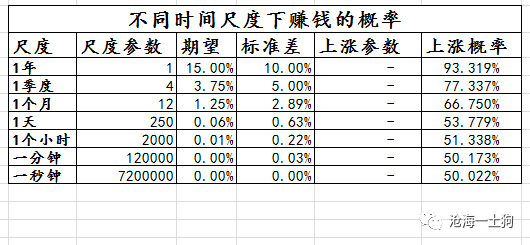
把所有的参数代入excel公式,我们计算出:1年看一次账户,看到账户上涨的概率为93.319%;如果一季度看一次账户,看到账户上涨的概率为77.337%;如果一个月看一次账户,看到账户上涨的概率为66.75%;如果一天看一次账户,看到账户上涨的概率为53.779%;以此类推,最后,一秒钟看一次账户,看到账户上涨的概率为50.022%。
**看账户的频率越高,结果就越接近于掷硬币** ,所以,一秒钟看一次账户,结果跟掷硬币的结果差不多。即使一天看一次,结果也好不到哪里去。
**时效性和准确性的取舍**
综上所述,对于包含随机性因素的现象,在构建组合时候,我们必然会面临时效性和准确性的取舍,单纯地偏向某一个极端都不会有太好的结果。
太偏向于准度,最可能的结果就是,过于保守,买一堆持有到期的利率债啥都不干;太偏向于时效性,最可能的结果就是,像前文《 [ 散户输光定律
](http://mp.weixin.qq.com/s?__biz=MzUxNjE1NjI1MA==&mid=2247484090&idx=1&sn=3796050844eda27be0d17ce72bc24364&chksm=f9aafc8fcedd75996b46fea203d37e5dcfbf84a78093ae812f52e6794a5464fb8d48010b04e7&scene=21#wechat_redirect)
》中那样,被市场反复收割,最后,因为资金有限,亏完离场。
所以,我们需要某种折中,预测的尺度不能太大,更不能太小。譬如说,单纯从股票市场的预测而言,预测准度存在这样一个排序:预测明天a股票会涨 <
预测明天b组合会涨 < 预测一段时间内c组合会涨。
前两者因为尺度太小,受到经济活动中的“热运动”的干扰太大,所以,前面两者往往表现出“布朗运动”的态势,很难预测准确。但是,“预测一段时间内c组合”会上涨,就不同——
随着组合c标的种类的扩大以及观察时间的拉大, **“热运动”的噪音会被过滤掉** ,于 是,我们就更有可能提出比较靠谱的 **因果论断** 。
> 在充满不确定的世界里,较大尺度是因果论断存在的前提。
>
> ——土狗按
**自下而上投资的局限**
基于上面的讨论,我们不难发现,自下而上投资的微观局限在哪里,有太多的基于微观的预测,受噪音的扰动太大,预测的效果惨不忍睹。
此外,大家选股票的策略不是 **准度更高的排除法** ,往往用的是直接选择的方法。在前文《 [ 如何做好投资中的送分题
](http://mp.weixin.qq.com/s?__biz=MzUxNjE1NjI1MA==&mid=2247484045&idx=1&sn=c8ce7a1566cc5ec4278d5af108fdac7c&chksm=f9aafcb8cedd75ae05fdee03f3c6c701dca8cba4b0951dc23fdba75ec88fc277278e956da48f&scene=21#wechat_redirect)
》中,我们介绍过排除法指数增强。在这里,我们再引用一遍:
以平庸的沪深300指数为基准,首先,选择出基本面预期最差的5%,准确度为δ,预期增强收益为γ;如果我们不满足预期增强收益γ,就需要扩大剔除的范围,比如说,剔掉预期基本面最差的10%,准确度δ会降低。
在这个框架下,我们会发现另外一对矛盾体, **增强收益的幅度γ和准确度δ** ,这两者负相关。
可是,自下而上的思路往往忽略了准确度δ这个因素,他们直接去选择他们认为最好的top10,即最好的3%,准确度δ往往是低得让人感动。
所以,一般而言,自下而上投资、精选个股的思路,往往会在准确度上栽跟头。他们选股的准度跟掷硬币差不多,无论在时间上还是数量上的组合尺度又太小,秉持这种思路的账户表现往往表现出极大的异质性:有很好的,有很差的,也有很多中庸的。
表现很好的投资经理往往会吹嘘自己精选个股策略的阿尔法,但是,基于小尺度组合的逻辑,我们不难判断出,这种不均匀只是随机现象的一种表现罢了,因为参与这个游戏的投资经理足够多,出现几个特别好的,没什么奇怪的。
> 抬头看看看看四周,你就会发现瞎猫,他们脸上洋溢着幸福而自信的笑容。
>
> ——土狗按
**阿尔法的存在性**
或许,有些人会对瞎猫( _ 幸运的傻瓜 _ )的说法愤愤不平,觉得阿尔法反映了投资水平,那么,我们找一个可控制的随机事件,给大家提供一些直觉。
我们找一个均匀的九宫格,然后,蒙上白纸,往上扔飞镖。假设我们有9只飞镖,每只飞镖落到某一个格子里的概率是确定的,都是1/9。
随便进行一次实验,我们会发现,总有一些格子里没有飞镖,有些格子里有两个及以上的飞镖。这种结果并非我们原来内心可能预期的“每个格子一只飞镖”。难道我们能基于这样的一次实验去说,有三只飞镖的格子的阿尔法是2,有0只飞镖的格子的阿尔法是-1么?
显然,这是一件极其愚蠢的事情。然而,不幸的是,我们对于基金经理的评价体系,往往是这样的逻辑。大家往往会忽略一个事实,公募基金的基金经理大都年轻,平均任职期限不超过一轮牛熊。
此外,如果我们把格子扩大到16格,飞镖的数目扩大到16支,我们会发现,出现一只格子有更多的飞镖的概率增大,即不同格子飞镖数目的异质性增强。这个现象对应于,随着参与这个游戏的投资经理数目的增加,市场会越来越容易出现阿尔法特别高的投资经理和组合——幸运的傻瓜会越来越多。
> 随着时间的拉长,尺度的增加,所有精选个股的阿尔法都会还原成贝塔。
>
> ——土狗按
**更加复杂的现实**
前面的随机性问题仅仅是基于被人类驯服了的随机性,是我们 **认识世界的拐棍** 罢了,实际的随机性更加不可捉摸。
因为有预期和非理性情绪等因素的存在,金融资产的价格表现更加狂暴不安,金融资产的价格和成交量表现出了极高的自相关性,并且,金融资产的成交量也远高于“市场有效假说”情况下的理论值。
在这种情况下, **即便是通过增加标的种类和时间扩大尺度也未必能获得一个确定的“因果关系”** ,预测的准度因此也极其低下,自下而上投资的困难将更加复杂。
最后,我们就以一个展示现实世界随机过程复杂性的小案例收尾吧:
还是九宫格,我们以键盘打字的九宫格为例。不同的语种,每个格子被点击的频率是不一样的,举个未必准确的例子,中文可能是2号键,英文可能是7号键;不同职业的人也可能不同;不同年龄的人也可能不同;不同性别的人也可能不同。所以,随便统计100次按键,不同人的随机模式会有很大的不同——
** 千万不要低估随机模式的种类 ** 。
> 一个债券交易员,可能6号键比较常用,他总是tkn和gvn;但是,一个北京老大爷,2号键却比较常用。
>
> ——土狗按
End

预览时标签不可点
微信扫一扫
关注该公众号
****
****
× 分析
收藏
# 自下而上投资的局限:经济活动的测不准原理
原创 沧海一土狗 [ 沧海一土狗 ](javascript:void\(0\);)
__ _ _ _ _
**

文/沧海一土狗 ** ** **
**引子**
不久之前,跟一位业内的老前辈聊天,谈论起了投资方法论的问题,是应该“自上而下”投资,还是应该“自下而上”投资?
由于我们两个都是做固定收益出身的,所以,对自上而下的投资方法有着天然的亲近感。当时,我也只是单纯地在自己的方法论里打转,前辈的一句话,让我有茅塞顿开的感觉:
> 自下而上的投资方法, ** 只适合宏观环境比较平稳的时候 ** ,当宏观环境变化剧烈的时候,这个方法会很惨,就比如今年。
基于这样的逻辑,我们不难推断,随着中国资本市场的开放,更多的国际因素会影响到国内宏观环境,造成其波动加剧,自下而上投资方法受到的限制会越来越大。
在现实中,有很多人喜欢给自己立flag——我就碰到过好多自称“自上而下”的基金经理。这些flag只给他们带来“抱团”的虚假安全感,环境一旦骤变,他们面临的只是团灭。
资本市场自然选择的力量是无情的,被工具绑架,不注重工具或者方法 **使用条件** 的人最终是要被淘汰的。
**宏观和微观的区别**
跟前辈的探讨激发了我更多的思考,宏观和微观的真实区别是什么?恰好在这段时间里,我读了一些物理学的科普读物,其中的案例以 **不同的视角**
向我展现了,宏观和微观的界限。
_**气体磁化实验** _
如果在一个长方形的石英管里注入氧气,并且把它放进磁场,你就会发现气体被磁化了。由于氧分子是一些小的磁体,于是,他们就会像指南针似的始终与磁场保持平行的趋势,这样我们就看到气体磁化的现象。
直觉上人们会认为它们都与磁场的单一方向平行,其实不是这样。如果你增加磁场,氧气中的磁化作用也随之增强,更多的氧气分子就会趋于这个方向。磁化效应会随着磁场强度的增加而增加,它们之间是一种正比例的关系。

氧气分子的方向是杂乱无章的,他受两种力量的影响。宏观方面,单个氧气分子受到确定方向的磁场影响;微观方面,单个氧气分子不断地遭到 热运动
的随机取向的干扰。
尽管单个分子总是无休止的改变取向,然而,由于他们数量庞大,所以总体上来看,趋于场强方向的比例还是多于其他方向。
如何在物理上进一步验证统计假说呢?如果磁化现象的确是磁场力量和热运动随机干扰的某种平衡,那么,我们就 **可以通过降低温度来代替加强磁场**
。现实实验中,我们也的确发现了这一现象。
通过这个实验,我们可以发现,一方面,我们无法在微观上观测一些分子的朝向,也无法对他们的方向进行预测;另一方面,我们的确也能发现
**在宏观上存在一些确定的因果规律** 。微观的不可预测性和宏观的确定性以这样一种形式,完美地结合在一起。
除此之外,在布朗运动、扩散现象中,我们也可以发现,微观不确定性和宏观确定性的某种结合。在沉降的雾气中,微小的水珠运动轨迹表现出不规则的布朗运动,但是,受重力的影响,雾气总体还是分布在下层;在扩散运动中,虽然我们无法知晓某一个分子酒精分子的运动轨迹,但我们可以知晓酒精分子总体上会从浓度大的趋于扩散至浓度小的区域。

对于任意一个截面,任一个酒精分子从左侧穿越到右侧的概率,与从右侧穿越到左侧的概率是一样的。所以,当且仅当左侧酒精分子浓度和右侧酒精浓度一致时,宏观上来看,酒精浓度才不会出现变化;但是微观上来看,任意时刻总有一部分酒精分子从左侧运动到右侧,也有一部分从右侧到左侧,只不过
** 他们的数量接近一致罢了 ** 。
**尺度决定精度**
那么, **不可预测的微观个体是如何表现出确定性的宏观规律的呢?两者是如何的完美的结合在一起的呢?** 关于这一点,统计学可以给出一个解答。
对于n次掷硬币的实验(正面向上记成1,反面向上记成0),这个实验的期望EX=n/2,方差DX=n/4 。如果我们掷m次硬币,并
预测有多少次正面上,一个合理的预测就是他的期望m/2。
那么,这个 **预测的误差** 是多少呢?我们可以拿(标准差/期望)这个变量来计量误差,即误差是1/根号m
。也就是说,m越大这个预测越准,而且准度是以根号n的速度收敛的。( _ 所以,统计学上有个根号n原则 _ )
通过这个例子,我们就可以获得一种直觉,对于组成个体符合某种随机性的组合,组合越大,就越可能产生某种可以预测的行为,组合越小,就越受随机性的干扰。
> 尺度越大,预测越准。
>
> ——土狗按
**时效性和准确性的矛盾**
> 从长期看,我们都死了。
>
> ——凯恩斯
凯恩斯这句名言告诉我们,在某些问题上,单纯地追求准度——100%正确,对于我们可能毫无意义。现实中还有很多其他的例子,譬如,预测北京明年夏天一定会下雨,预测a股十年内一定会出现一波上涨。尽管这些预测会很准确,但他缺乏时效性。
现实当中, **人们除了会走准确度的极端之外,还会走时效性的极端**
。譬如,人们总是想预测明天的股市是上涨还是下跌?但是,因为尺度太小,预测的准度相当差,几乎相当于掷硬币。
在以前的文章《 [ 如何在充满噪音的世界里生存?
](http://mp.weixin.qq.com/s?__biz=MzUxNjE1NjI1MA==&mid=2247484472&idx=1&sn=e177f70eb522b146487f1e86c01dce9b&chksm=f9aafa0dcedd731b394d2303278b733e59d09c9611ef3f7036f01407bc62710d4e485a3ec3a3&scene=21#wechat_redirect)
》一文中,我们举过一个例子,我们这里再引用一下:
假设有一个投资高手,他一年期望的报酬率是15%,波动性(标准差)为10%,也就是说,一年下来这个投资高手的收益率大概率在5%和25%之间波动。
我们再假设他的报酬率符合正态分布的话,那么,他年收益落在5%和25%之间的概率为68%。此外,我们也可以很容易的算出,他年收益率大于零的概率为93%。
这时候就有一个很自然的问题,如果这个高手每季度看一次组合,他看到某一个季度组合收益上涨的概率是多少?
为了回答这个问题,我们再引入一个假设, **每季度的收益率独立同分布,** **且都是正态分布。**

根据上面的数学推导,我们可以算出任意切片事件收益率的分布。然后,我们把参数代入公式,就可以计算在 ** 不同时间尺度上 ** ,赚钱的概率,

把所有的参数代入excel公式,我们计算出:1年看一次账户,看到账户上涨的概率为93.319%;如果一季度看一次账户,看到账户上涨的概率为77.337%;如果一个月看一次账户,看到账户上涨的概率为66.75%;如果一天看一次账户,看到账户上涨的概率为53.779%;以此类推,最后,一秒钟看一次账户,看到账户上涨的概率为50.022%。
**看账户的频率越高,结果就越接近于掷硬币** ,所以,一秒钟看一次账户,结果跟掷硬币的结果差不多。即使一天看一次,结果也好不到哪里去。
**时效性和准确性的取舍**
综上所述,对于包含随机性因素的现象,在构建组合时候,我们必然会面临时效性和准确性的取舍,单纯地偏向某一个极端都不会有太好的结果。
太偏向于准度,最可能的结果就是,过于保守,买一堆持有到期的利率债啥都不干;太偏向于时效性,最可能的结果就是,像前文《 [ 散户输光定律
](http://mp.weixin.qq.com/s?__biz=MzUxNjE1NjI1MA==&mid=2247484090&idx=1&sn=3796050844eda27be0d17ce72bc24364&chksm=f9aafc8fcedd75996b46fea203d37e5dcfbf84a78093ae812f52e6794a5464fb8d48010b04e7&scene=21#wechat_redirect)
》中那样,被市场反复收割,最后,因为资金有限,亏完离场。
所以,我们需要某种折中,预测的尺度不能太大,更不能太小。譬如说,单纯从股票市场的预测而言,预测准度存在这样一个排序:预测明天a股票会涨 <
预测明天b组合会涨 < 预测一段时间内c组合会涨。
前两者因为尺度太小,受到经济活动中的“热运动”的干扰太大,所以,前面两者往往表现出“布朗运动”的态势,很难预测准确。但是,“预测一段时间内c组合”会上涨,就不同——
随着组合c标的种类的扩大以及观察时间的拉大, **“热运动”的噪音会被过滤掉** ,于 是,我们就更有可能提出比较靠谱的 **因果论断** 。
> 在充满不确定的世界里,较大尺度是因果论断存在的前提。
>
> ——土狗按
**自下而上投资的局限**
基于上面的讨论,我们不难发现,自下而上投资的微观局限在哪里,有太多的基于微观的预测,受噪音的扰动太大,预测的效果惨不忍睹。
此外,大家选股票的策略不是 **准度更高的排除法** ,往往用的是直接选择的方法。在前文《 [ 如何做好投资中的送分题
](http://mp.weixin.qq.com/s?__biz=MzUxNjE1NjI1MA==&mid=2247484045&idx=1&sn=c8ce7a1566cc5ec4278d5af108fdac7c&chksm=f9aafcb8cedd75ae05fdee03f3c6c701dca8cba4b0951dc23fdba75ec88fc277278e956da48f&scene=21#wechat_redirect)
》中,我们介绍过排除法指数增强。在这里,我们再引用一遍:
以平庸的沪深300指数为基准,首先,选择出基本面预期最差的5%,准确度为δ,预期增强收益为γ;如果我们不满足预期增强收益γ,就需要扩大剔除的范围,比如说,剔掉预期基本面最差的10%,准确度δ会降低。
在这个框架下,我们会发现另外一对矛盾体, **增强收益的幅度γ和准确度δ** ,这两者负相关。
可是,自下而上的思路往往忽略了准确度δ这个因素,他们直接去选择他们认为最好的top10,即最好的3%,准确度δ往往是低得让人感动。
所以,一般而言,自下而上投资、精选个股的思路,往往会在准确度上栽跟头。他们选股的准度跟掷硬币差不多,无论在时间上还是数量上的组合尺度又太小,秉持这种思路的账户表现往往表现出极大的异质性:有很好的,有很差的,也有很多中庸的。
表现很好的投资经理往往会吹嘘自己精选个股策略的阿尔法,但是,基于小尺度组合的逻辑,我们不难判断出,这种不均匀只是随机现象的一种表现罢了,因为参与这个游戏的投资经理足够多,出现几个特别好的,没什么奇怪的。
> 抬头看看看看四周,你就会发现瞎猫,他们脸上洋溢着幸福而自信的笑容。
>
> ——土狗按
**阿尔法的存在性**
或许,有些人会对瞎猫( _ 幸运的傻瓜 _ )的说法愤愤不平,觉得阿尔法反映了投资水平,那么,我们找一个可控制的随机事件,给大家提供一些直觉。
我们找一个均匀的九宫格,然后,蒙上白纸,往上扔飞镖。假设我们有9只飞镖,每只飞镖落到某一个格子里的概率是确定的,都是1/9。
随便进行一次实验,我们会发现,总有一些格子里没有飞镖,有些格子里有两个及以上的飞镖。这种结果并非我们原来内心可能预期的“每个格子一只飞镖”。难道我们能基于这样的一次实验去说,有三只飞镖的格子的阿尔法是2,有0只飞镖的格子的阿尔法是-1么?
显然,这是一件极其愚蠢的事情。然而,不幸的是,我们对于基金经理的评价体系,往往是这样的逻辑。大家往往会忽略一个事实,公募基金的基金经理大都年轻,平均任职期限不超过一轮牛熊。
此外,如果我们把格子扩大到16格,飞镖的数目扩大到16支,我们会发现,出现一只格子有更多的飞镖的概率增大,即不同格子飞镖数目的异质性增强。这个现象对应于,随着参与这个游戏的投资经理数目的增加,市场会越来越容易出现阿尔法特别高的投资经理和组合——幸运的傻瓜会越来越多。
> 随着时间的拉长,尺度的增加,所有精选个股的阿尔法都会还原成贝塔。
>
> ——土狗按
**更加复杂的现实**
前面的随机性问题仅仅是基于被人类驯服了的随机性,是我们 **认识世界的拐棍** 罢了,实际的随机性更加不可捉摸。
因为有预期和非理性情绪等因素的存在,金融资产的价格表现更加狂暴不安,金融资产的价格和成交量表现出了极高的自相关性,并且,金融资产的成交量也远高于“市场有效假说”情况下的理论值。
在这种情况下, **即便是通过增加标的种类和时间扩大尺度也未必能获得一个确定的“因果关系”** ,预测的准度因此也极其低下,自下而上投资的困难将更加复杂。
最后,我们就以一个展示现实世界随机过程复杂性的小案例收尾吧:
还是九宫格,我们以键盘打字的九宫格为例。不同的语种,每个格子被点击的频率是不一样的,举个未必准确的例子,中文可能是2号键,英文可能是7号键;不同职业的人也可能不同;不同年龄的人也可能不同;不同性别的人也可能不同。所以,随便统计100次按键,不同人的随机模式会有很大的不同——
** 千万不要低估随机模式的种类 ** 。
> 一个债券交易员,可能6号键比较常用,他总是tkn和gvn;但是,一个北京老大爷,2号键却比较常用。
>
> ——土狗按
End

预览时标签不可点
微信扫一扫
关注该公众号
****
****
× 分析
收藏