# 人性深处的缺陷——小样本谬误
原创 沧海一土狗 [ 沧海一土狗 ](javascript:void\(0\);)
__ _ _ _ _
**

文/沧海一土狗 ** ** **
**引子**
在《韩非子-
五蠹》里有个小故事,大意是,宋国有个农民,他的田地中有一截树桩。一天,一只跑得飞快的野兔撞在了树桩上,扭断了脖子死了。于是,农民便放下他的农具日日夜夜守在树桩子旁边,希望能再得到一只兔子。然而野兔是不可能再次得到了,而他自己也被宋国人耻笑。这就是我们大家熟知的“
**守株待兔** ”的故事。虽然这个故事比较搞笑,但是,他反映了人性当中的一种缺陷—— **认识世界,过于依赖小样本** 。
对于“守株待兔”这件事情,我们可以一目了然的知晓,兔子再撞死在树桩上的概率很低,所以,宋国人很蠢。但是,对于那些看起来靠谱一点的事情呢?我们的表现会比那么宋国人更好吗?这一篇,我们将探讨一下这个问题。
**赌徒谬误**

在轮盘赌中,看到一长串的红色之后,大多数人错误地相信现在应该是黑色了;在重复抛一枚公平的硬币时,如果连续多次抛出反面朝上,人们可能会错误地认为,下一次抛出正面的机会比较大。这种现象被称为“
** 赌徒谬误 ** ”。总之,赌徒谬误是指相信某一个特定的结果由于最近已发生了(“运气用尽了”)或最近没有发生(“交霉运”),再发生的机会会较低。
赌徒谬误产生的原因在于人们错误地解释了“大数定律”的平均法则,他们认为,几率存在一个 **自我校正**
的过程,其中一个方向的偏离,将诱发相反方向的偏离以维持平衡。
如果连续抛出了5次反面向上( _抛出正面记为1,反面记为0_ ),那么,人们倾向于认为很快就有多次正面向上来 **校正这种偏离**
。实际上,大数定律的中,样本的期望是0.5,不是被“校正”的,而是被“稀释”的。
连续5次反面向上的 ** 5格序列 ** 出现的几率只有1/32,与他不同的5格序列的 **种类多达31个。**
下一个时间段,无论哪一个序列出现的几率都只是1/32。如果抛100次硬币,会出现 ** 更多种 **
不同于“5次反面向上”的5格序列,最终会导致反面出现的次数被稀释到占50%左右。
**等比例的理想世界**

通过上面的讨论,我们不难发现,人们总是 **低估了序列的种类,而高估了小样本的代表性,并认为总体是小样本的某种等比例放大。**
假设我们把掷硬币的序列扩张到10格序列,序列的种类将达到1024种。如果你请一个人随机作出一个10格序列,那么,这个序列的期望值很可能是0.5附近,很少有人会写出10次正面或10次反面这种序列。他们会认为,那两种极端情况出现的几率太低,只有不到千分之一,但是,他们忘记了,他们写下的
** 任何一种序列出现的几率都低于千分之一 ** 。
所以,人们内心深处存在一种倾向,认为小样本和总体存在某种 **比例联系** 。换言之,人们认为某些小样本可以很好的 ** 代表总体 **
——总体是均匀的,是这些小样本的某种重复。然而,事实上,构成总体的样本千奇百怪,种类繁多,它并不是代表性小样本的重复,而是, ** 多种小样本的大杂烩
** 。
**对样本规模缺乏敏感性**

既然基于小样本的思考问题那么多,那么,为什么人们还是倾向于拿小样本说事?一方面是因为数据匮乏;另一方面是因为人们本身对样本规模就不敏感。在卡尼曼和特沃斯基(1972年b)的一篇文章里有这么一个案例:
> _
> 某镇有两个医院,大医院每天约45名婴儿出生,小医院每天约15名婴儿出生。众所周知,约50%的婴儿应该是男孩。但每天男孩出生的实际比例都不一样,有时高于50%,有时低于50%。
> _
>
> _ 在一年内,每家医院都记录新生儿中男孩比例大于60%的天数。请问你哪家医院会记录更多这样的天数? _
>
> _ 1、大医院(21) _
>
> _ 2、小医院(21) _
>
> _ 3、大致相同(也就是在5%的范围内)(53) _
>
> _ 括号中的数值,是选择该答案的大学生被试者的数目。 _
根据这个实验,我们发现,大部分被试者都认为,60%以上的新生儿是男孩的概率,在大医院和小医院都是一样的。他们似乎是认为,既然这个事件是按照同样的逻辑形成的,大一些的样本和小一些的样本都是总体的某种缩放,同样代表了一般的整体。
事实上,抽样理论则要求60%以上的新生儿是男孩的天数,更可能是在小医院发生的, **因为大样本更不可能偏离50%**
。样本的规模显然是重要的,但实际上,人们在思考的过程中,对样本规模并不敏感。
为了进一步探索人们对样本规模的缺乏敏感性, 卡尼曼和特沃斯基进一步构作了另外一个实验,
> _
> 一个容器装满小球,其中2/3是一种颜色,1/3是另外一种颜色。一个人从容器中拿出5个球,结果发现4个是红的,1个是白的。另一个人从容器中拿出20个球,结果发现12个是红的,8个是白的。谁会对“容器里的球2/3是红的,而1/3是白的”更有信心?每个人给出的几率应该是多少?
> _
根据计算,第一个人红对白的几率是8对1;第二个人红对白的几率是16对1
。然而,受试的大多数人则认为第一个样本提供了更强的证据,支持容器中有更多红球的假设,因为 ** 红球的比例 ** 在第一个样本中比第二个样本中更大。
** 直觉判断再次受到样本比例的主宰,忽视了样本规模的影响 ** 。
**投资中的小样本问题**
由于人们是按照 ** 线性外推的模式 ** 思考问题的,所以, **人们倾向于认为总体是具备某种代表性的小样本的缩放**
,忽视了小样本的多样性,更忽视了样本规模的影响。
在投资当中,这种倾向也十分明显,譬如,市场在经历了很多下跌之后,投资者倾向认为市场很快就要触底反弹了;一个投资者通过某种特定的模式赚钱之后,会期望该模式会重复(
** _守株待兔的翻版_ **
),并且可以继续通过该模式赚到钱。然而,在经历漫长下跌之后,市场的后序序列是极其多样的,未必会立马通过更多的上涨来纠正过多的下跌;偶然赚钱的模式,也未必具备可重复性。
关于简单的离散的概率问题,小样本思路就已经很难把握清楚,更何况复杂性更高的金融时间序列数据。
布莱恩-阿瑟在1994年提出了一个很著名的问题——“爱尔法鲁酒吧”的问题,来模拟金融市场的非均衡性,
> _
> 在圣塔菲的峡谷路,有一家名为“爱尔法鲁”的酒吧。每个星期四晚上,酒吧都会有表演。人们如果预期那里人不多,他们就会去;如果预期那里人很拥挤,他们就不去。这会导致一个很有意思的决策问题:“很多人会去酒吧”这种预测会导致几乎没人去,而“不会有什么人去酒吧”这种预测则会导致许多人去。这意味着理性预期——
> _ ** _ 正确或有效的预测,会导致自我否定 _ ** _ 。 _
在这样一个非均衡预期的市场上,去酒吧的人数会出现极其剧烈的波动。这种波动毫无规律可言,可能的时间序列种类超过人们的想象,甚至所谓的大样本也只能在某些变量上保持稳定——平均到场人数会收敛到酒吧的
** 座位数 ** 。
基于这样的逻辑,我们有理由对以下的两个命题保持良好的怀疑:1、金融时间序列是某些序列片段的重复;2、简单模式的缩放和有限组合可以很好地描述市场。
**结束语**
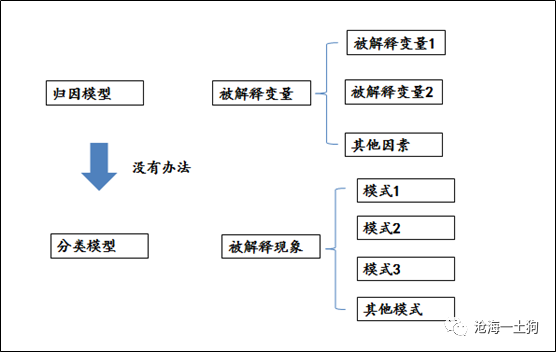
人们总是有冲动去解释一切现象,然而,从本质上来讲, **解释现象是一种压缩信息的行为** 。
首先,我们可能想到的压缩办法就是构建模型对这个 ** 现象归因 ** ;如果做不出模型,就 ** 对现象分类 **
,然后划分模式,通过不同模式来理解现象。尽管后者较前者的难度有所降低,但是,后者的难度一点都不小——它要求解释者掌握所有模式之间的规律。
但是,在随机性的世界里,且不说模式的种类过于繁多,模式与模式之间的相关性也可能是存疑的—— ** 信息具备不可压缩性 **
。这一切会给我们带来了很大的麻烦——我们解释现象的冲动让我们去压缩信息,这种被迫的压缩带来信息丢失,但我们的很多决策又是基于这种极为失真的信息。
这一系列的失误造成了一种现象,人们总是 ** 不愿意容忍自己不知道某件事的原因,并根据这种不知道作出决策 **
,总是不断地通过“具备代表性”小样本简单重复的模式来理解总体,可是,在某些情况下,这种决策机制带来的后果是灾难性的。
最后的结论有点过于悲观,所以,拿投资界的老前辈查理-芒格的两句话结尾吧:
> _聪明人也不免遭受_ ** _过度自信_ ** _带来的灾难。他们认为自己有更强的能力和更好的办法,所以,他们往往就在_ **
> _更加艰难的道路上疲于奔命_ ** _。_
>
> _承认自己不懂某样东西,意味着_ ** _智慧的曙光_ ** _即将来临。_
>
> _——查理-芒格_
图片来自网络
End

预览时标签不可点
微信扫一扫
关注该公众号
****
****
× 分析
收藏
原创 沧海一土狗 [ 沧海一土狗 ](javascript:void\(0\);)
__ _ _ _ _
**

文/沧海一土狗 ** ** **
**引子**
在《韩非子-
五蠹》里有个小故事,大意是,宋国有个农民,他的田地中有一截树桩。一天,一只跑得飞快的野兔撞在了树桩上,扭断了脖子死了。于是,农民便放下他的农具日日夜夜守在树桩子旁边,希望能再得到一只兔子。然而野兔是不可能再次得到了,而他自己也被宋国人耻笑。这就是我们大家熟知的“
**守株待兔** ”的故事。虽然这个故事比较搞笑,但是,他反映了人性当中的一种缺陷—— **认识世界,过于依赖小样本** 。
对于“守株待兔”这件事情,我们可以一目了然的知晓,兔子再撞死在树桩上的概率很低,所以,宋国人很蠢。但是,对于那些看起来靠谱一点的事情呢?我们的表现会比那么宋国人更好吗?这一篇,我们将探讨一下这个问题。
**赌徒谬误**

在轮盘赌中,看到一长串的红色之后,大多数人错误地相信现在应该是黑色了;在重复抛一枚公平的硬币时,如果连续多次抛出反面朝上,人们可能会错误地认为,下一次抛出正面的机会比较大。这种现象被称为“
** 赌徒谬误 ** ”。总之,赌徒谬误是指相信某一个特定的结果由于最近已发生了(“运气用尽了”)或最近没有发生(“交霉运”),再发生的机会会较低。
赌徒谬误产生的原因在于人们错误地解释了“大数定律”的平均法则,他们认为,几率存在一个 **自我校正**
的过程,其中一个方向的偏离,将诱发相反方向的偏离以维持平衡。
如果连续抛出了5次反面向上( _抛出正面记为1,反面记为0_ ),那么,人们倾向于认为很快就有多次正面向上来 **校正这种偏离**
。实际上,大数定律的中,样本的期望是0.5,不是被“校正”的,而是被“稀释”的。
连续5次反面向上的 ** 5格序列 ** 出现的几率只有1/32,与他不同的5格序列的 **种类多达31个。**
下一个时间段,无论哪一个序列出现的几率都只是1/32。如果抛100次硬币,会出现 ** 更多种 **
不同于“5次反面向上”的5格序列,最终会导致反面出现的次数被稀释到占50%左右。
**等比例的理想世界**

通过上面的讨论,我们不难发现,人们总是 **低估了序列的种类,而高估了小样本的代表性,并认为总体是小样本的某种等比例放大。**
假设我们把掷硬币的序列扩张到10格序列,序列的种类将达到1024种。如果你请一个人随机作出一个10格序列,那么,这个序列的期望值很可能是0.5附近,很少有人会写出10次正面或10次反面这种序列。他们会认为,那两种极端情况出现的几率太低,只有不到千分之一,但是,他们忘记了,他们写下的
** 任何一种序列出现的几率都低于千分之一 ** 。
所以,人们内心深处存在一种倾向,认为小样本和总体存在某种 **比例联系** 。换言之,人们认为某些小样本可以很好的 ** 代表总体 **
——总体是均匀的,是这些小样本的某种重复。然而,事实上,构成总体的样本千奇百怪,种类繁多,它并不是代表性小样本的重复,而是, ** 多种小样本的大杂烩
** 。
**对样本规模缺乏敏感性**

既然基于小样本的思考问题那么多,那么,为什么人们还是倾向于拿小样本说事?一方面是因为数据匮乏;另一方面是因为人们本身对样本规模就不敏感。在卡尼曼和特沃斯基(1972年b)的一篇文章里有这么一个案例:
> _
> 某镇有两个医院,大医院每天约45名婴儿出生,小医院每天约15名婴儿出生。众所周知,约50%的婴儿应该是男孩。但每天男孩出生的实际比例都不一样,有时高于50%,有时低于50%。
> _
>
> _ 在一年内,每家医院都记录新生儿中男孩比例大于60%的天数。请问你哪家医院会记录更多这样的天数? _
>
> _ 1、大医院(21) _
>
> _ 2、小医院(21) _
>
> _ 3、大致相同(也就是在5%的范围内)(53) _
>
> _ 括号中的数值,是选择该答案的大学生被试者的数目。 _
根据这个实验,我们发现,大部分被试者都认为,60%以上的新生儿是男孩的概率,在大医院和小医院都是一样的。他们似乎是认为,既然这个事件是按照同样的逻辑形成的,大一些的样本和小一些的样本都是总体的某种缩放,同样代表了一般的整体。
事实上,抽样理论则要求60%以上的新生儿是男孩的天数,更可能是在小医院发生的, **因为大样本更不可能偏离50%**
。样本的规模显然是重要的,但实际上,人们在思考的过程中,对样本规模并不敏感。
为了进一步探索人们对样本规模的缺乏敏感性, 卡尼曼和特沃斯基进一步构作了另外一个实验,
> _
> 一个容器装满小球,其中2/3是一种颜色,1/3是另外一种颜色。一个人从容器中拿出5个球,结果发现4个是红的,1个是白的。另一个人从容器中拿出20个球,结果发现12个是红的,8个是白的。谁会对“容器里的球2/3是红的,而1/3是白的”更有信心?每个人给出的几率应该是多少?
> _
根据计算,第一个人红对白的几率是8对1;第二个人红对白的几率是16对1
。然而,受试的大多数人则认为第一个样本提供了更强的证据,支持容器中有更多红球的假设,因为 ** 红球的比例 ** 在第一个样本中比第二个样本中更大。
** 直觉判断再次受到样本比例的主宰,忽视了样本规模的影响 ** 。
**投资中的小样本问题**
由于人们是按照 ** 线性外推的模式 ** 思考问题的,所以, **人们倾向于认为总体是具备某种代表性的小样本的缩放**
,忽视了小样本的多样性,更忽视了样本规模的影响。
在投资当中,这种倾向也十分明显,譬如,市场在经历了很多下跌之后,投资者倾向认为市场很快就要触底反弹了;一个投资者通过某种特定的模式赚钱之后,会期望该模式会重复(
** _守株待兔的翻版_ **
),并且可以继续通过该模式赚到钱。然而,在经历漫长下跌之后,市场的后序序列是极其多样的,未必会立马通过更多的上涨来纠正过多的下跌;偶然赚钱的模式,也未必具备可重复性。
关于简单的离散的概率问题,小样本思路就已经很难把握清楚,更何况复杂性更高的金融时间序列数据。
布莱恩-阿瑟在1994年提出了一个很著名的问题——“爱尔法鲁酒吧”的问题,来模拟金融市场的非均衡性,
> _
> 在圣塔菲的峡谷路,有一家名为“爱尔法鲁”的酒吧。每个星期四晚上,酒吧都会有表演。人们如果预期那里人不多,他们就会去;如果预期那里人很拥挤,他们就不去。这会导致一个很有意思的决策问题:“很多人会去酒吧”这种预测会导致几乎没人去,而“不会有什么人去酒吧”这种预测则会导致许多人去。这意味着理性预期——
> _ ** _ 正确或有效的预测,会导致自我否定 _ ** _ 。 _
在这样一个非均衡预期的市场上,去酒吧的人数会出现极其剧烈的波动。这种波动毫无规律可言,可能的时间序列种类超过人们的想象,甚至所谓的大样本也只能在某些变量上保持稳定——平均到场人数会收敛到酒吧的
** 座位数 ** 。
基于这样的逻辑,我们有理由对以下的两个命题保持良好的怀疑:1、金融时间序列是某些序列片段的重复;2、简单模式的缩放和有限组合可以很好地描述市场。
**结束语**

人们总是有冲动去解释一切现象,然而,从本质上来讲, **解释现象是一种压缩信息的行为** 。
首先,我们可能想到的压缩办法就是构建模型对这个 ** 现象归因 ** ;如果做不出模型,就 ** 对现象分类 **
,然后划分模式,通过不同模式来理解现象。尽管后者较前者的难度有所降低,但是,后者的难度一点都不小——它要求解释者掌握所有模式之间的规律。
但是,在随机性的世界里,且不说模式的种类过于繁多,模式与模式之间的相关性也可能是存疑的—— ** 信息具备不可压缩性 **
。这一切会给我们带来了很大的麻烦——我们解释现象的冲动让我们去压缩信息,这种被迫的压缩带来信息丢失,但我们的很多决策又是基于这种极为失真的信息。
这一系列的失误造成了一种现象,人们总是 ** 不愿意容忍自己不知道某件事的原因,并根据这种不知道作出决策 **
,总是不断地通过“具备代表性”小样本简单重复的模式来理解总体,可是,在某些情况下,这种决策机制带来的后果是灾难性的。
最后的结论有点过于悲观,所以,拿投资界的老前辈查理-芒格的两句话结尾吧:
> _聪明人也不免遭受_ ** _过度自信_ ** _带来的灾难。他们认为自己有更强的能力和更好的办法,所以,他们往往就在_ **
> _更加艰难的道路上疲于奔命_ ** _。_
>
> _承认自己不懂某样东西,意味着_ ** _智慧的曙光_ ** _即将来临。_
>
> _——查理-芒格_
图片来自网络
End

预览时标签不可点
微信扫一扫
关注该公众号
****
****
× 分析
收藏